comment faire des 1/3 propres en perspective ?

Bonjour !  

Je ne sais pas ou je dois poster ce genre de questions.

En perspective j'ai compris comment faire des moitiés propres avec les diagonales mais je n'arrive pas à faire de même pour "couper" une distance en 3.
est-ce qu'il y a un moyen sans avoir à mesurer ? et sans faire de l'approximatif ?
et souvent le découpage en "impair" est plus équilibré.

Merci

Si je ne me gourre pas (c'est parti loin la pers', depuis le début de l'année ! ), il suffit de créer une "règle" faite d'un segment que tu aura copié trois fois, à partir de l'origine de la portion que tu veut segmenter (très important de placer ta règle sur ce point).
Ensuite tu projette l'extrémité de cette règle sur l'extrémité de ton objet (1), pour trouver ton point de mesure sur l'horizon (2), et à partir de là tu projette les autres points vers ce point de mesure (3).
Puis tu tire les verticales ou bien t'en fais ce que tu veux quoi !  

Merci beaucoup Virid

il faut donc passer par le mesure.
cette méthode est valable quand on a une distance que l'on veut multiplier par 3 ou plus ...
mais pour diviser par trois une ligne donnée ? je vais essayer "à l'envers" :
il faut que je fasse le report sur une ligne "droite" "en face" de nous. et que je divise par 3 la longueur obtenue ...

Encore Merci

Non je multiplie pas là, je divise. En l’occurrence j'ai divisé la face du pavé vert (qui était déjà là) en 3.

Ca c'est multiplier (en bleu) :

Ah OK merci !
j'avais compris comme ça :
longeur quelconque x3 puis faire sur l'axe choisi !
et non, surface verte d'abord, puis coupée en 3 ! (c'est ce que je voulais faire)


Merci, Virid, tes explications sont claires

Bon ça fait longtemps que la question a été posée, mais on ne sait jamais si ça peut servir à quelqu'un.
Pour éviter de mesurer, on peut aussi utiliser cette méthode pour diviser un rectangle ou autre volume en 3 parties égales. J'ai trouvé cela dans un vieux bouquin de perspective récemment:



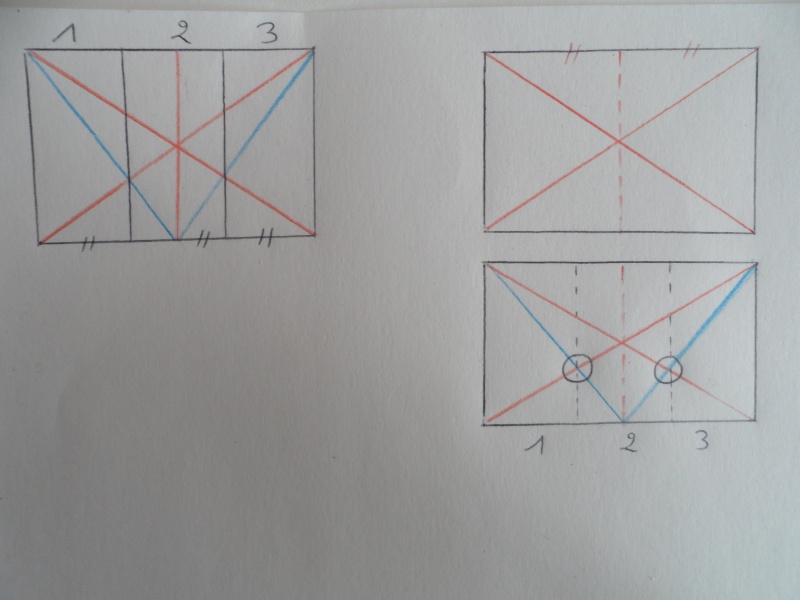
Donc en gros il faut couper la surface en deux en traçant les diagonales (rouge), et ensuite une fois qu'on a obtenu les deux parties égales on trace une diagonale dans chacune de ces deux parties (bleu), et on découpe en trois là où les diagonales rouge et bleu se croisent.

Et après il n'y a plus qu'à faire la même chose mais en perspective.